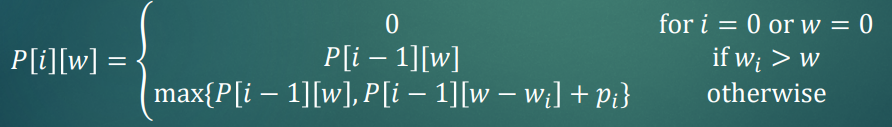알고리즘(Java) - Knapsack Problem을 알아보자.
요약
Knpasack Problem은 보통 배낭 문제로 불리며 여러 바리에이션이 존재한다. 대표적인 바리에이션인 분할 가능한 아이템을 사용한 배낭 문제는 그리디 알고리즘을 이용하여 해결할 수 있다.
하지만 분할 가능하지 않은 아이템을 사용할 경우 완전 탐색과 다이나믹 프로그래밍 중 시간 복잡도를 비교하여 선택할 수 있다. 다이나믹 프로그래밍에서 최적 부분 문제를 찾기 까다로운 문제이지만 i번째 아이템에서 w 무게 제한으로 얻을 수 있는 최대 가치(P[i][w])가 부분 문제임을 알고 있으면 쉽게 구현할 수 있다.
Knapsack Problem
Knapsack Problem의 전체적인 구성은 다음과 같다.
- W 무게까지 담을 수 있는 가방이 주어진다.
- 무게와 가치가 주어진 물건들을 가방에 담는다.
- 이 가방에 담은 물건들의 가치 합이 최대가 되는 물건들을 찾아야 한다.
이 구성에서 여러 조건을 추가하여 Knapsack Problem의 다양한 바리에이션을 만들 수 있다.
- 물건을 잘라서 담을 수 있는 경우(빵, 금가루 등)
- 동일한 물건을 여러 개 담을 수 있는 경우
- 가방이 여러 개인 경우
가장 먼저 물건을 자를 수 있는 경우를 생각해보자.
Fractional Knapsack Problem
도둑은 한정된 가방으로 가장 많은 금액은 훔쳐야 한다. 이 때 가방의 공간이 부족한 경우 보석을 잘라서 일부만 가져갈 수 있다고 할 때 어떻게 들고가야 할까?
그리디 알고리즘에서 가장 중요한 것은 어떻게 뽑아야 최적해가 될 수 있는지 판단하는 것이다. 단순히 무게 상관없이 가장 비싼 물건만 뽑는다고 하면 최적해가 될 수 없다. 이 경우에서 무게가 30 lb이고 150$인 물건이 추가된다고 하면 쉽게 반례를 생각해볼 수 있다.
Fractional Knapsack Problem에서 그리디 알고리즘을 적용할 수 있는 방법은 바로 무게 당 가치가 제일 높은 물건부터 선택하는 것이다. 최적 부분 구조(optional substructure)와 탐욕적 선택 속성(greedy choice property)를 확인하여 그리디 알고리즘이 항상 최적해를 보임을 확인하자. 계속 탐욕적 선택을 하면 최적해가 성립되는 최적 부분 구조임은 쉽게 알 수 있으므로 탐욕적 선택 속성을 확인해보자.
탐욕적 선택 속성
만약에 어떤 최적해가 탐욕적 선택 속성을 가지지 않는다고 하자. 예를 들어 가장 처음에 선택된 물건이 무게 당 가치가 제일 높은 물건이 아니라고 할 때 그 물건을 무게 당 가치가 제일 높은 물건으로 변경하면 전체 가치를 높일 수 있다.
이게 가능한 이유는 물건을 잘라서 넣을 수 있으므로 무게 당 가치를 제일 높은 물건으로 항상 변경할 수 있기 때문이다. 따라서 이 문제는 탐욕적 선택 속성을 만족한다.
0-1 Knapsack Problem
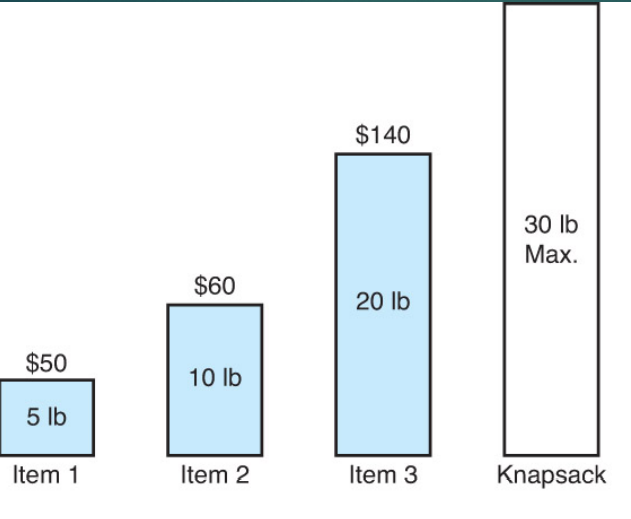
0-1 Knapsack Problem은 이전과 달리 보석을 잘라서 가져갈 수 없다. Fractinal Knapsack Problem 예제에서 보석을 잘라서 가져갈 수 없다고 할 때 똑같이 그리디 알고리즘을 적용해보자.
이 경우 item 3를 먼저 선택하고 item 1을 선택하는 것이 그리디 알고리즘의 해이다. 하지만 item 2 + item 3일 때 전체 가치가 더 높다. 따라서 기존의 그리디 알고리즘으로 0-1 Knapsack Problem을 해결할 수 없다.
Brute Force
그럼 모든 경우의 수를 고려하면 어떨까? 모든 item 당 가방에 담거나 담지 않는 두 가지 선택지가 있다. 따라서 item이 n개이면 2^n의 경우의 수가 존재한다. 이는 n이 조금만 커져도 시간이 매우 오래 걸리게 된다.
Dynamic Programming
다이나믹 프로그래밍으로 해결하기 위해서는 그리디 알고리즘과 동일하게 최적 부분 구조를 찾아야 한다. 부분 문제를 다음과 같이 적용해보자.
P[i][w]는 1 ~ i번째 아이템(i <= 전체 아이템 수 n)으로 w 무게의 배낭(w <= 가방 크기 W)에 담을 수 있는 최대 가치이다. 이 P[i][w]로 P[n][W]를 구할 수 있다. P[i][w]는 다음과 같은 3가지 케이스로 나눌 수 있다.
- i = 0 이거나 w = 0이면 P[i][w]는 0이다.
- i번째 아이템이 무게 w를 초과하면 i번째 아이템을 담을 수 없으므로 P[i][w] = P[i-1][w]이다.
- i번째 아이템을 담을 수 있으면 i번째 아이템을 포함한 전체 가치와 i번째 아이템을 포함하지 않은 전체 가치 중 최대값이 P[i][w]이다. (P[i][w] = max{P[i-1][w], P[i-1][w-wi] + pi)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int[] line = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int N = line[0]; int K = line[1];
items = new int[N+1][2];
memo = new int[N+1][K+1];
for (int i = 0; i < N; i++) {
items[i+1] = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
}
//case 1은 배열 초기화 때 자동으로 0으로 배치
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= K; j++) {
if (items[i][0] > j) memo[i][j] = memo[i-1][j]; //case 2
else {
//case 3
memo[i][j] = Math.max(memo[i-1][j], memo[i-1][j - items[i][0]] + items[i][1]);
}
}
}
System.out.print(memo[N][K]);
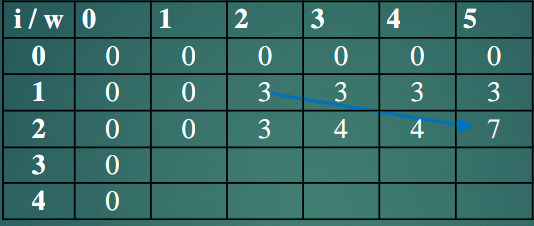
Case 3의 예시를 표로 확인해보면 다음과 같다.
(Weight, Value)
- (2, 3)
- (3, 4)
- (4, 5)
- (5, 6)
item 2의 무게는 3으로 P[2][5]에서 w인 5보다 작으므로 3번 케이스에 속한다. 따라서 item 2를 포함했을 때와 포함하지 않았을 때를 비교해서 최대값을 가져 오면 된다.
- item 2 포함 : P[2][5] = P[1][2] + item[2][1] = 3 + 4 = 7
- item 2 포함하지 않음 : P[2][5] = P[1][5] = 3
따라서 P[2][5]의 값은 7이 된다.
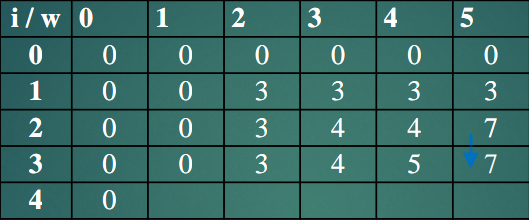
item 3의 무게는 4로 P[3][5]에서 w인 5보다 작으므로 마찬가지로 3번 케이스이다. 이 때 item 3을 포함하는 것이 이득인지 아닌지 살펴볼 수 있다.
- item 3 포함 : P[3][5] = P[2][1] + item[3][1] = 0 + 5 = 5
- item 3 포함하지 않음 : P[3][5] = P[2][5] = 7
이 경우는 item 3를 포함하지 않는 것이 이득임을 확인할 수 있다.
이렇게 P[n][W]까지 구하면 배낭에 담을 수 있는 최대 이익을 구할 수 있다.
결론
이렇게 보면 O(2^n)인 완전 탐색보다 다이나믹 프로그래밍이 훨씬 빠른 것처럼 보인다. 하지만 다이나믹 프로그래밍도 W가 아주 큰 특수한 경우에는 오히려 완전 탐색보다 느릴 수 있다. 따라서 시간 복잡도를 미리 확인하여 어떤 방식을 사용할 지 결정해야 한다.
다이나믹 프로그래밍의 경우 (n+1)(W+1) 크기의 배열을 만들어 한번 순회하므로 O(nW)의 시간 복잡도를 가진다. 이 때 W가 n!과 같이 아주 큰 수를 가지고 있다면 nW가 2^n보다 커질 수 있는 것이다. 그러므로 W가 아주 크고 n이 작은 경우에는 완전 탐색이 효율적이고 W가 작고 n이 큰 경우는 다이나믹 프로그래밍이 더 효율적이다. 이를 고려하고 문제를 푼다면 최적의 알고리즘을 선택할 수 있다.
연관 문제
Reference
2022 1학기 알고리즘 수업 자료, PNU Visual & Biometric Computing Laboratory