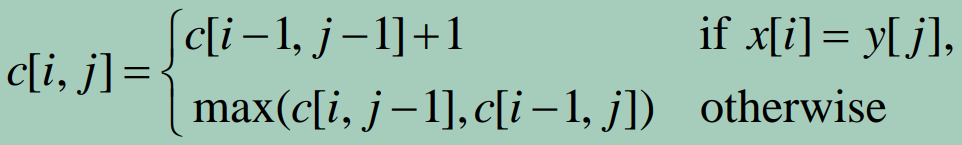알고리즘(Java) - LCS(Longest Common Subsequence) 문제를 알아보자.
요약
LCS 문제는 두 수열의 최장 공통 부분 수열을 찾아야 한다. 이 문제는 최적화된 부분 문제를 가지고 있다. X와 Y 일부분(prefix)의 LCS를 찾은 결과는 X와 Y의 LCS를 찾을 때 재활용된다. 따라서 이는 다이나믹 프로그래밍으로 해결할 수 있다. LCS를 찾기 위해 브루트 포스를 사용하면 O(N2^N)의 시간 복잡도를 가지지만 다이나믹 프로그래밍을 사용하면 O(N^2)으로 해결할 수 있다.
LCS
LCS 개론
LCS(Longest Common Subsequence) 문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 여기서 수열은 원소들이 정렬되어 있는 리스트이다. 순서가 중요하다는 말이다. 한 수열에서 몇 개의 원소들을 제거하되 남은 원소의 순서를 유지했을 경우 부분 수열이라고 한다.
- ACTTGCG
- ACT, ATTC, T, ACTTGC는 모두 ACTTGCG의 부분 수열이 될 수 있다.
따라서 두 수열의 부분 수열을 비교하여 일치하는 부분 수열 중 가장 긴 수열을 찾으면 되는 문제이다. 이러한 LCS 문제는 니들만-브니쉬 알고리즘(Needleman-Wunsch Algorithm)과 같이 DNA, 단백질 서열 정렬로도 확장된다.
브루트 포스로 해결하기
이 문제를 해결하기 위해 두 수열의 모든 부분 수열을 찾아 일치하는지 비교해보는 방법이 있다. 문제는 한 수열의 모든 부분 수열을 찾는 경우의 수가 너무 많다는 것이다. 수열 X의 길이를 M, 수열 Y의 길이를 N으로 하자. 이 때 X의 부분 수열은 2^M개 존재한다.
Y의 부분 수열은 굳이 찾지 않고 Y를 순회하면서 X의 부분 수열 내 모든 원소가 Y에 존재하고 순서까지 맞는지 확인하면 된다. 이 때 Y를 한 번 순회하므로 부분 수열 하나 당 O(N) 시간이 소요된다.
따라서 브루트 포스의 시간 복잡도는 O(N * 2^M)이다. 지수 함수로 증가하므로 N과 M이 아주 작지 않은 이상 브루트 포스로 해결하면 아주 많은 시간이 걸릴 것이다.
최적화된 부분 문제
모든 다이나믹 프로그래밍 문제는 최적화된 부분 문제를 찾아서 재활용하는 것에서 시작된다. 다음과 같은 두 수열이 있다고 하자.
- X : ABAC
- Y : ABCD
X와 Y는 모두 prefix + 한글자로 분리할 수 있다. X는 ABA/C, Y는 ABC/D로 말이다. 이 prefix는 또 prefix의 prefix + 한글자로 분리할 수 있다. X의 prefix는 AB/A와 Y의 prefix는 AB/C로 분리할 수 있다. X와 Y 수열의 LCS(최적 해)를 이 prefix(부분 문제)의 LCS(최적 해)에서 구할 수 있다면 이는 최적화된 부분 문제라 볼 수 있다.
이 LCS가 최적화된 부분 문제를 가진다는 점을 이용하여 해결해보자.
LCS 길이 구하기
X.i는 길이가 i인 X의 prefix이고 Y.j는 길이가 j인 Y의 prefix라고 하자. 그리고 c[i, j]는 X.i와 Y.j의 LCS 길이이다. 이 때 LCS 길이의 점화식은 다음과 같다.
경우의 수 1
c[i-1, j-1]를 알고 있고 X[i] = Y[j]이라면 c[i, j]은 얼마일까? 어렵지 않게 c[i, j] = c[i-1, j-1] + 1임을 유추할 수 있다. 아래 그림에서 c[4, 2]은 3(CTC)이고 c[5, 3]은 4(CTCA)가 된다.
경우의 수 2
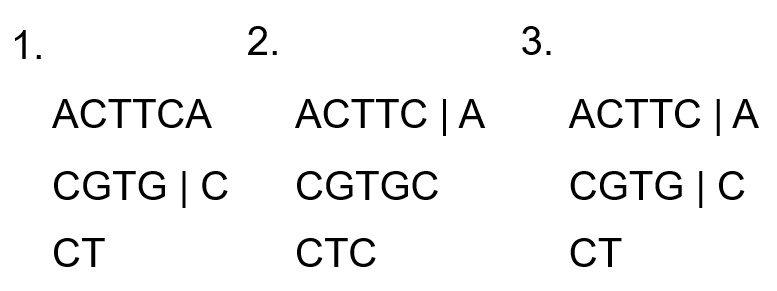
X[i] != Y[j]라면 어떻게 구할 수 있을까? X[i] != Y[j]는 X[i] “또는” Y[j]는 LCS에 포함되지 않는다고 이해할 수 있다. “또는”을 강조한 이유는 둘 중 하나가 LCS에 포함될 수 있기 때문이다. 아래 그림의 2번에서 Y[j]의 C는 LCS에 포함됨을 확인할 수 있다.
따라서 X[i]와 Y[j] 둘 중 하나는 LCS에 포함될 가능성을 염두해야 한다. 그러므로 우리는 그림의 3번처럼 c[i, j] = c[i-1, j-1]으로 계산하면 안된다. 그림의 1번과 2번처럼 X[i]나 Y[j]가 LCS에 포함될 가능성을 둘 다 계산해본 후 최대값을 가져와야 한다. c[i, j] = max(c[i, j-1], c[i-1, j])로 최대값을 가져올 수 있다.
LCS 길이 코드
1
2
3
4
5
6
7
8
9
10
11
12
int m = X.length();
int n = Y.length();
int[][] c = new int[m+1][n+1];
//i = 0일 때 빈 수열이고 i = 1일 때 X[0]과 동일하므로 charAt에서 인덱스를 1 빼줘야 한다.
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (a.charAt(i-1) == b.charAt(j-1)) c[i][j] = c[i-1][j-1] + 1;
else c[i][j] = Math.max(c[i-1][j], c[i][j-1]);
}
}
시간 복잡도
길이가 m과 n인 2차원 배열을 한번 순회하므로 시간 복잡도는 O(m * n)이다.
LCS 문자열 구하기
LCS 문자열의 길이가 아닌 LCS 문자열 그 자체를 구하고 싶다면 어떻게 해야할까? 다음과 같은 그림을 확인하면 더 쉽게 이해할 수 있다.
대각선 화살표의 의미는 다음과 같다. 대각선 화살표 시작 위치를 c[i][j]이고 끝 위치가 c[i-1][j-1]이라고 할 때 c[i-1][j-1] + 1 = 1이다. c[i-1][j] + 1 = c[i][j], c[i][j-1] + 1 = c[i][j]도 만족한다. 이 말은 X[i]도 LCS에 포함되고 Y[j]도 LCS에 포함된다는 말이다. 따라서 c[i][j] != c[i-1][j], c[i][j] != c[i][j-1]을 모두 만족하면 X[i]와 Y[j] 모두 LCS에 포함된다고 보고 X[i]나 Y[j]를 출력하면 된다.
그럼 왼쪽 화살표의 의미는 무엇일까? c[i][j] = c[i-1][j] + 1, c[i][j] = c[i][j-1]이다. Y[j]는 LCS에 포함되지 않지만 X[i]는 LCS에 포함된다는 뜻이다. 따라서 Y[j]는 출력할 필요가 없으므로 j를 1 빼서 좌측으로 이동하면 된다.
반대로 위쪽 화살표인 경우는(테이블 그림에는 없지만) X[i]를 출력할 필요가 없으므로 i를 1 빼서 우측으로 이동하면 된다.
이를 정리하면 다음과 같다.
c[i][j] != c[i-1][j], c[i][j] != c[i][j-1]이다
-> X[i]와 Y[j] 모두 LCS에 포함되므로 출력하고 c[i-1][j-1]로 이동한다.(대각선 화살표)
c[i][j] == c[i-1][j], c[i][j] != c[i][j-1]이다
-> Y[j]만 LCS에 포함되므로 c[i][j-1]로 이동하여 X[i]는 버린다.(위쪽 화살표)
c[i][j] != c[i-1][j], c[i][j] == c[i][j-1]이다
-> X[i]만 LCS에 포함되므로 c[i-1][j]로 이동하여 Y[j]는 버린다.(왼쪽 화살표)
1 ~ 3번을 i = m-1, j = n-1에서 시작하여 i나 j가 0이 될 때까지 반복하면 된다. 이 때 역순으로 출력되므로 한번 뒤집어 주어야 한다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int i = m;
int j = n;
StringBuilder sb = new StringBuilder();
while (i != 0 && j != 0) {
//1번
if (c[i][j] != c[i-1][j] && c[i][j] != c[i][j-1]) {
sb.insert(0, a.charAt(i-1)); //1 빼줘야 한다. 맨 앞에 삽입하여 역순 출력 대체
i--;
j--;
}
//2번
else if (c[i][j] != c[i][j-1]) i--;
else j--;
}
return sb.toString();
결론
LCS의 길이를 구할 때는 점화식을 활용하여 테이블을 채워나가면 된다. LCS의 문자열을 구할 때에는 c[m][n]에서 출발하여 c[i][j] != c[i-1][j] && c[i][j] != c[i][j-1]인 지점에서 X[i]를 역순으로 출력하는 방식으로 해결할 수 있다.
연관 문제
Reference
2022 1학기 알고리즘 수업 자료, PNU Visual & Biometric Computing Laboratory