알고리즘(Java) - 프림 알고리즘을 알아보자.
요약
프림 알고리즘은 그리디 알고리즘을 기본으로 하여 최소 신장 트리를 찾을 수 있는 알고리즘이다. 이 때까지 선택된 정점과 연결된 모든 간선들 중 가장 가중치가 작은 간선을 탐욕적으로 선택한다. 이 후 가장 가중치가 작은 간선의 다른 한 정점을 선택한 후 다시 이전의 과정을 반복한다. 두 정점이 모두 선택된 간선은 포함될 수 없다는 점을 기억하면 어렵지 않게 구할 수 있다.
서론
백준 문제 풀이를 하던 중 골드 1~3의 문제들 중 최소 신장 트리를 활용하는 문제가 많아 이에 관해 정리해보았다. 프림 알고리즘과 크루스칼 알고리즘 두 가지 알고리즘이 있는데 이번 포스트에서는 프림 알고리즘에 대해서만 알아보기로 한다. 최소 신장 트리의 개념을 먼저 정리하고, 프림 알고리즘의 구현 방식을 예제를 들어 설명할 것이다.
크루스칼 알고리즘과 두 알고리즘의 비교는 다음 포스트에서 알아볼 예정이다.
최소 신장 트리
신장 트리(Spanning Tree)
어떠한 그래프 G = (V, E)가 주어졌다고 하자. 이 때 V는 정점(Vertex)의 집합이고 E는 간선(Edge)의 집합이다.
한 그래프의 부분 그래프 G`는 다음과 같이 정의한다. G` = (V`, E`)에서 V`는 V의 부분 집합, E`는 E의 부분 집합이다.(단 E`에서 모든 간선은 V` 내의 정점들을 연결해야 한다.)
신장 트리(Spanning Tree)의 정의는 다음과 같다.
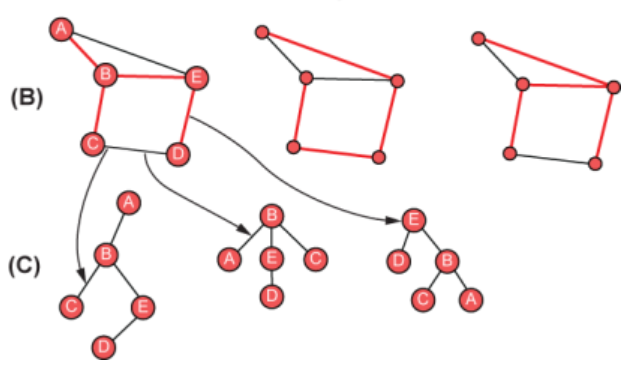
- 신장 트리는 G = (V, E)의 부분 그래프 G` = (V, E`)이다. 즉, 기존 그래프의 모든 정점을 포함해야 한다.
- G`는 트리의 정의를 만족해야 한다.(acyclic, connected, undirected) 그러므로 간선의 개수 |E`|는 |V| - 1개이다.
(B)와 같이 하나의 그래프는 여러 개의 신장 트리를 가질 수 있다.
최소 신장 트리(Minimum Spanning Tree)
최소 신장 트리의 정의는 다음과 같다.
- 가중치를 가진 그래프 G로 신장 트리 G` = (V, E`)를 만들 때 E`의 모든 간선의 가중치 합이 최소가 되어야 한다.
이러한 최소 신장 트리는 흩어져 있는 기지국을 모두 연결할 때 인터넷 선을 가장 적게 사용하는 방법과 같은 경우에 활용할 수 있다. 이 최소 신장 트리를 찾는 대표적인 알고리즘이 프림과 크루스칼 알고리즘이다.
프림(Prim)의 알고리즘
프림의 알고리즘은 그리디(Greedy) 알고리즘을 바탕으로 한다. G` = (V`, E`)에서 |V`| == |V|가 될 때까지 최소 가중치를 가진 e를 선택하게 된다.
원리는 다음과 같다.
- 아무 노드를 시작 노드를 하여 V`에 넣는다.
- V`의 정점을 endpoint를 하는 간선들 중 최소 가중치인 간선 e를 찾는다. 이 때 주의할 점은 e의 한 endpoint는 V`에 포함되어야 하고 나머지 하나는 V`에 포함되지 않아야 한다.
- e를 E`에 넣는다.
- e에서 V`의 정점이 아닌 나머지 정점은 V`에 넣는다.
2, 3, 4 과정을 V` == V 가 될 때까지 반복한다.
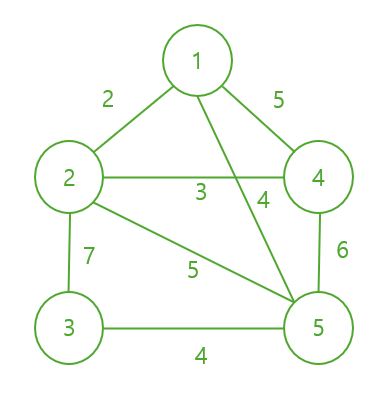
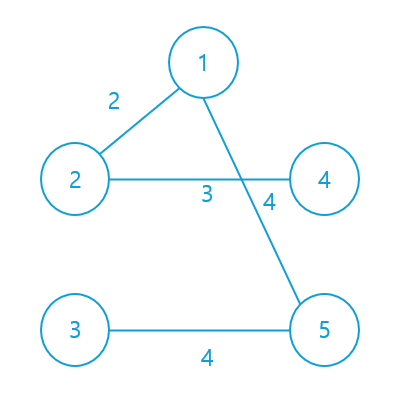
예시를 들어 자세히 알아보자. 다음과 같은 그래프 G가 있다.
시작 노드
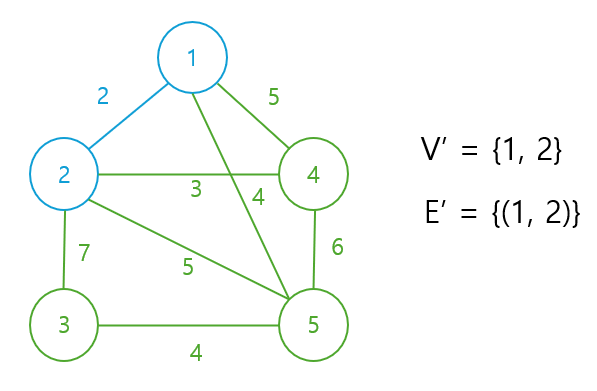
1번 정점을 시작 노드로 하여 V`에 넣는다.
두 번째 노드
V` = {1}의 정점을 endpoint로 하는 간선들 중 최소 가중치인 간선 e를 찾는다. 1을 endpoint로 하는 간선들 중 최소 가중치인 간선 e는 (1, 2), (1, 4), (1, 5) 중 가중치가 2인 (1, 2)이므로 e를 E`에 넣는다. 또한 나머지 endpoint 2를 V`에 넣는다.
세 번째 노드
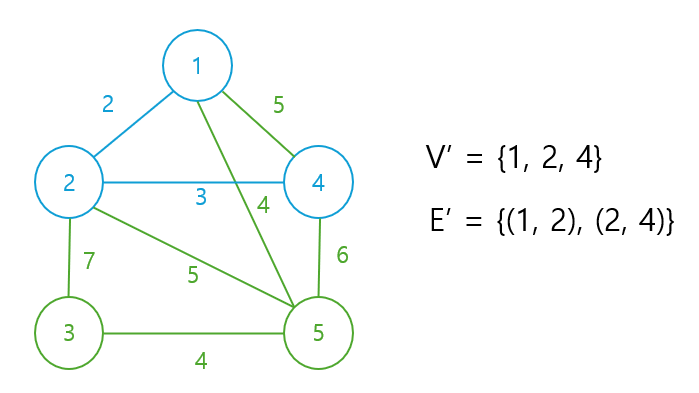
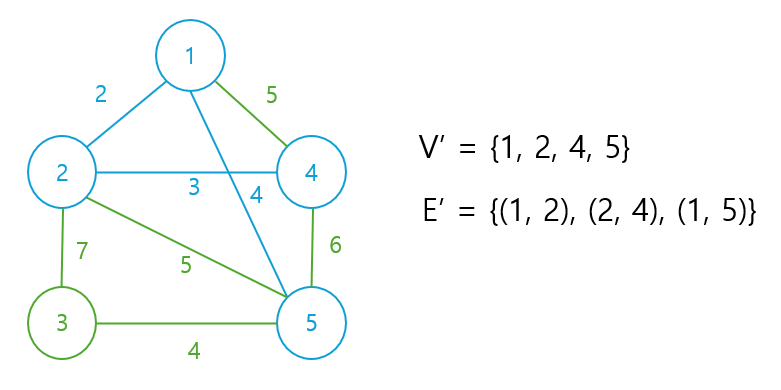
V` = {1, 2}의 정점 중 오직 하나만을 endpoint로 하는 간선들 중 최소 가중치인 간선 e를 찾는다. (1, 4), (1, 5), (2, 4), (2, 5), (2, 3) 간선 중 (2, 4)가 가중치가 3으로 최소이다. (2, 4)를 E`에 넣고 4를 V`에 넣는다.
네 번째 노드
V` = {1, 2, 3}의 정점 중 오직 하나만을 endpoint로 하는 간선들 중 최소 가중치인 간선 e를 찾는다. (1, 5), (2, 3), (2, 5), (4, 5) 간선 중 (1, 4)가 가중치가 4로 최소이다. (1, 4)를 E`에 넣고 5를 V`에 넣는다.
다섯 번째 노드
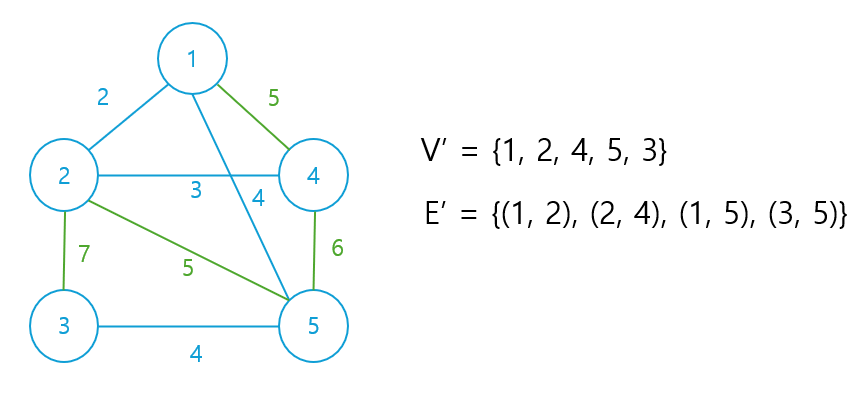
(2, 3), (3, 5) 간선 중 (3, 5)가 가중치가 4로 최소이다. (3, 5)를 E`에 넣고 3을 V`에 넣는다.
결과
V`의 크기가 V와 동일한 5이므로 더 이상의 탐색을 하지 않는다. 알고리즘의 결과로 선택된 간선은 다음과 같다.
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
long MinSumWeightWithPrimAlgorithm(List<List<Edge>> edgeInfo, int VertexNumber) {
int subVerticesSize = 0;
boolean[] vertices = new boolean[VertexNumber];
PriorityQueue<Edge> edges = new PriorityQueue<>();
//0에서 시작
vertices[0] = true;
subVerticesSize += 1;
List<Edge> startVertexEdgeInfo = edgeInfo.get(0);
for (Edge e : startVertexEdgeInfo) {
edges.add(e);
}
long sumOfWeight = 0;
while (subVerticesSize < VertexNumber) {
Edge minWeightEdge = edges.poll();
//간선의 endPoint 모두 V에 포함되어 있는 경우 건너뛰기
if (vertices[minWeightEdge.end]) continue;
//간선 가중치 더하기
sumOfWeight += minWeightEdge.weight;
//V에 포함되지 않은 정점 V에 추가하기(= 방문 처리하기)
vertices[minWeightEdge.end] = true;
subVerticesSize += 1;
//새로 포함되 V의 edge 전부 넣기
List<Edge> currentVertexEdgeInfo = edgeInfo.get(minWeightEdge.end);
for (Edge e : currentVertexEdgeInfo) {
edges.add(e);
}
}
return sumOfWeight;
}
class Edge implements Comparable<Edge> {
int end;
int weight;
Edge(int e, int w) {
end = e;
weight = w;
}
@Override
public int compareTo(Edge e) {
return weight - e.weight;
}
}
위의 코드는 프림 알고리즘을 이용하여 최소 신장 트리의 가중치 합을 구하는 문제이다. 가중치 합 대신 경로를 구하고 싶다면 우선순위 큐에서 나오는 간선들을 저장하면 된다.
현재 V`와 연결된 간선들 중 최소 가중치의 간선을 우선순위 큐를 이용하여 찾는다. 이 때 우선순위 큐에 endpoint 두 개 모두 V`에 포함되어 있는 경우를 체크하기 위해 vertices 배열을 활용한다. vertices[i]는 i번 째 정점이 V에 포함되었는지 여부를 반환한다.
시간 복잡도
인접 행렬
만약 간선을 인접 행렬의 형태로 저장했다면 매 방문한 정점마다 이 정점의 최소 간선을 찾는 연산을 수행한다. 모든 그래프의 정점은 한 번만 방문하므로 O(V^2)의 시간 복잡도를 가진다.
우선순위 큐
모든 정점은 한 번씩 거치므로 O(V)가 소요된다. 정점을 한번씩 거칠 때마다 최소 가중치 간선을 우선순위 큐에서 빼는 연산에 O(log E)가 소요된다. 이때 E는 최대 V(V - 1) / 2개 존재할 수 있으므로 빅오 표기법에 의해 O(log E) -> O(2log V) -> O(log V)로 간략화할 수 있다. 그러므로 모든 정점을 한번씩 거치며 최소 가중치 간선을 우선순위 큐에서 뺄 때 O(Vlog V)가 소요된다.
우선순위 큐에 간선을 추가할 때 최악의 경우 모든 간선이 최대 한 번씩 우선순위 큐에 추가될 수 있다. 모든 간선을 한 번씩 거칠 때 O(E)가 소요된다. 우선순위 큐의 삽입 연산의 시간 복잡도는 O(log V)이다. 그러므로 우선순위 큐에 간선을 추가할 때 시간 복잡도는 O(Elog V)이다.
우선순위 큐에 간선을 추가할 때와 최소 간선을 빼는 과정이 별개로 진행되기 때문에 최종 시간 복잡도는 O(Vlog V + Elog V)이다. 이는 E > V이므로 O(Elog V)로 간략화할 수 있다.
두 방식의 비교
이를 요약하면 간선의 수가 많으면 인접 행렬의 방식이, 간선의 수가 적으면 우선순위 큐의 방식이 더 좋다는 결론을 내릴 수 있다. 노드가 다른 모든 노드와 연결된 극단적인 경우 E = V(V-1) / 2가 되어 O(V^2log V)로 오히려 인접 행렬 방식보다 느릴 수도 있다.
결론
프림 알고리즘을 이용하면 최소 신장 트리를 어렵지 않게 구할 수 있다. 이는 그리디 알고리즘을 응용하여 매 부분 문제마다 V`의 정점을 endpoint를 하는 간선들 중 최소 가중치인 간선 e를 찾는 탐욕적 선택을 함으로써 구할 수 있다. 이 최소 가중치인 간선 e를 찾기 위해 보통 인접 행렬 방식과 우선순위 큐 방식을 사용한다. 이 중 간선의 수에 따라 어떤 방식을 사용할 지 선택하면 된다.
Reference
https://www.uvm.edu/~cbcafier/cs2240/content/14_mst/01_mst.html