알고리즘(Java) - 위상 정렬을 알아보자.
요약
위상 정렬에서 핵심은 진입차수이다.
- 진입차수가 0인 노드를 큐에 넣고 방문 처리한다.
- 큐에서 하나를 빼고 이와 연결된 주변 노드의 진입 차수를 1 감소시킨다.
- 다시 1, 2번 과정을 반복한다.
이러한 위상 정렬로 그래프에 사이클이 포함되어 있는지도 확인할 수 있다. 위상 정렬의 시간 복잡도는 O(V + E)이다.
서론
백준 1005 ACM Craft를 풀던 중 최장 거리에 관한 문제가 나왔다. 가중치가 존재할 때 최단 거리는 다익스트라로 쉽게 풀 수 있으므로 다익스트라의 갱신 부분만 수정하면 되지 않을까 생각했다. 하지만 이 경우 재방문하는 노드가 존재하기 때문에 시간 초과가 발생하였다.
찾아보니 위상 정렬을 사용하여 그래프의 최장 거리를 구할 수 있다고 한다. 위상 정렬은 생소한 개념이라 이 기회에 정리를 해보기로 한다.
이번 포스트에서는 위상 정렬에 대해서만 소개하고 다음 포스트에서 위상 정렬을 이용한 최장 거리를 소개할 예정이다.
위상 정렬
위상 정렬에서 대표적으로 소개하는 예시는 선수 과목이다. 어떤 과목을 듣기 위해서는 선수 과목이 필요하고 이 선수 과목은 하나 이상일 수 있다. 이 때 어떻게 들어야 선수 과목 이수를 지키면서 모두 이수할 수 있을지를 위상 정렬로 해결할 수 있다.
위상 정렬 용어의 기원
중요한 내용은 아니지만 흥미로운 글을 발견하여 소개한다. 두 가지 견해가 있는데 하나는 수학에서 위상이라는 개념이 과거 수가 아닌 모든 것을 포괄하는 용어였다. 이에 따라 위상 정렬은 수가 아닌 간선의 방향성으로 비교하므로 이를 위상으로 간주하여 명명되었다는 주장이 있다.
또 다른 견해는 컴퓨터 과학 초기에 네트워크의 구조를 위상으로 설명하는 데에서 유래되었다고 하는 견해이다.
따라서 첫 번째 주장에 따르면 오름차순, 내림차순처럼 수의 정렬이 아닌 간선의 방향성의 정렬이므로 수가 아닌 위상을 정렬하는 위상 정렬로 볼 수 있다. 또 다른 주장은 그래프(네트워크)를 위상으로 보아 위상인 그래프를 정렬하는 위상 정렬로 명명되었다는 견해이다.
위상 정렬의 정의
위상 정렬은 사이클이 없는 방향 그래프(DAG)에서 간선으로 주어진 정점 간 선후관계를 위배하지 않도록 나열하는 정렬이다. 사이클이 존재하게 되면 선후 관계를 정확히 정의할 수 없다. A -> B -> C -> A에서 A는 C의 선수과목이 되고 C는 A의 선수과목이 되는 모순이 발생한다.
위상 정렬의 결과는 또한 여러 답 중 하나만을 알려준다.
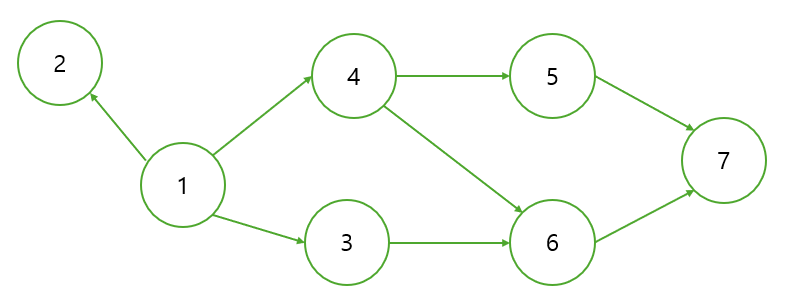
위와 같은 그래프의 경우 1234567이 가능하다. 또한 1245367도 가능하다. 위상 정렬은 이와 같은 많은 경우의 수 중 한 가지 답을 알려준다. 위의 그래프에서 1362457은 불가능하다. 6으로 가기 위해서는 3과 4를 먼저 방문해야 하기 때문이다.
위상 정렬의 구현
위상 정렬을 구현하기 위해서는 노드의 진입차수(indegree)와 진출차수(outdegree)를 알아야 한다. A 노드가 존재할 때 진입 차수는 다른 노드에서 A 노드로 향하는 간선의 수다. 반대로 진출차수는 A 노드에서 다른 노드로 향하는 간선의 개수이다.
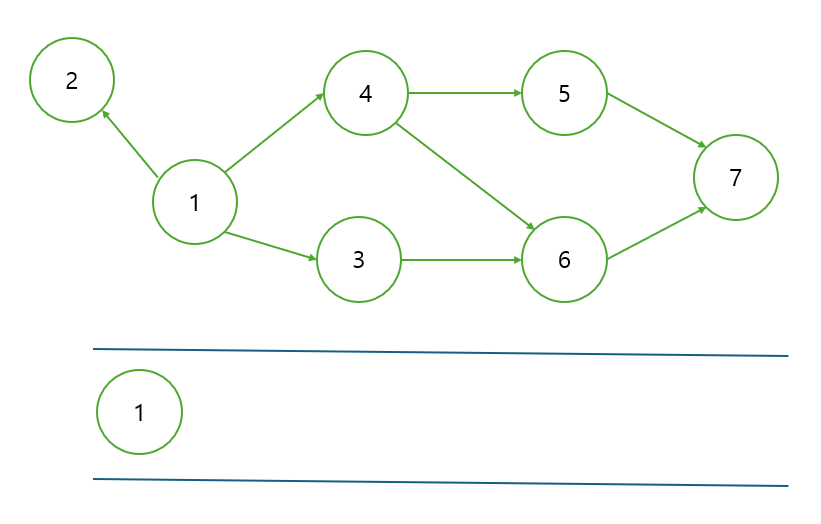
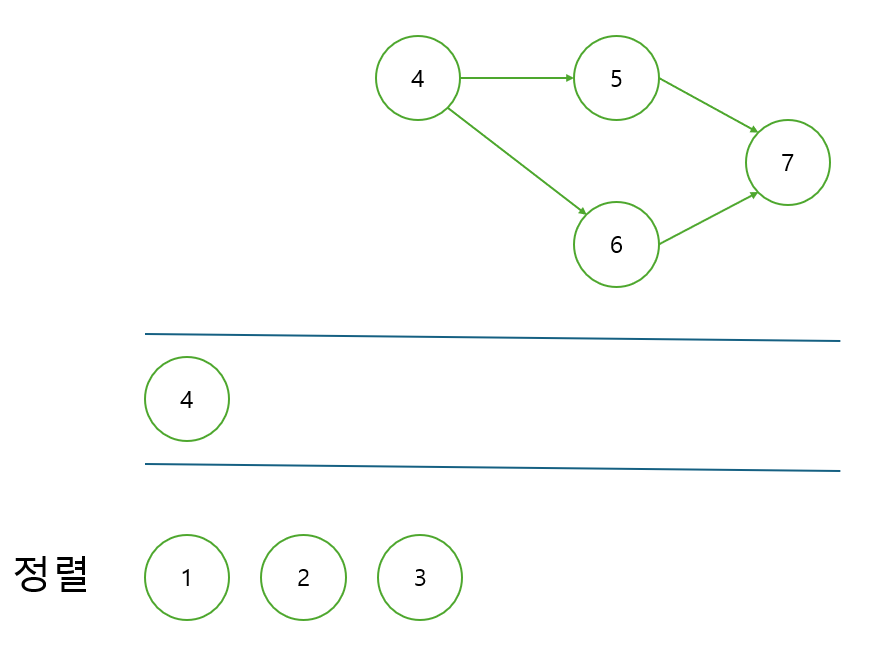
가장 처음으로 선택해야 하는 노드는 어떤 노드일까? 진입차수가 0이라면 선수 과목이 없다는 뜻이므로 바로 수강할 수 있다. 따라서 진입차수가 0인 노드를 선택한다.
1번 노드가 진입차수가 0이므로 선택하도록 하자. 한 노드에서 처리하는 과정은 다음과 같다.
과정 1. 진입차수가 0인 노드를 큐에 넣는다.
진입차수가 0인 노드는 선수 과목을 모두 이수하여 수강할 수 있는 노드로 보면 된다.
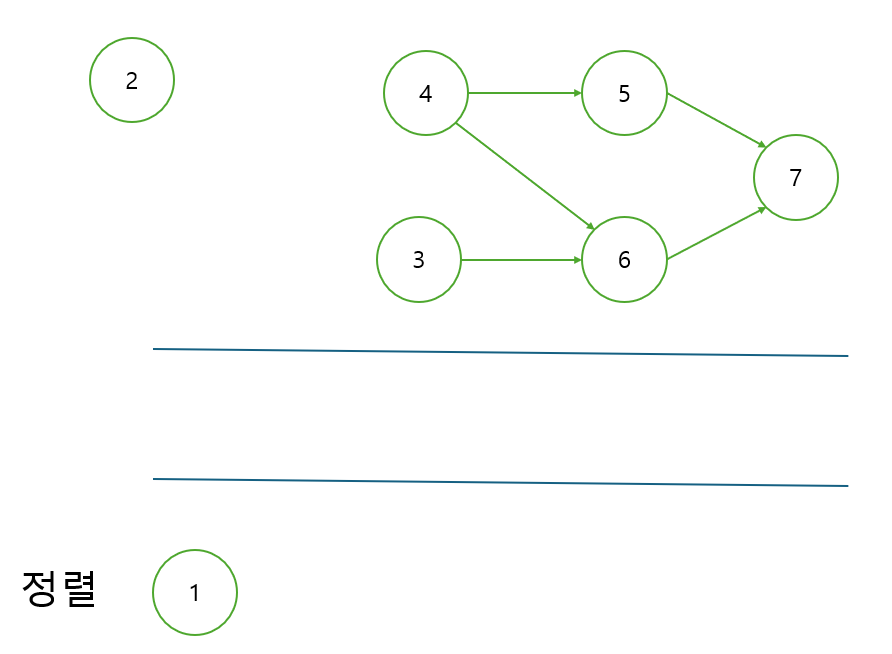
과정 2. 큐에 있는 노드를 빼고 주변 간선을 제거하는 과정을 거친다.
주변 간선을 제거하는 과정은 선수 과목을 이수했다는 뜻으로 봐도 된다. 큐에서 뺀 노드는 정렬 값으로 저장하면 된다.
과정 3. 모든 노드를 방문할 때까지(큐가 빌 때까지) 과정 1과 과정 2를 반복한다.
과정 2에서 진입차수가 0인 노드는 2, 3, 4이다. 따라서 이 세 개의 노드를 넣으면 된다.
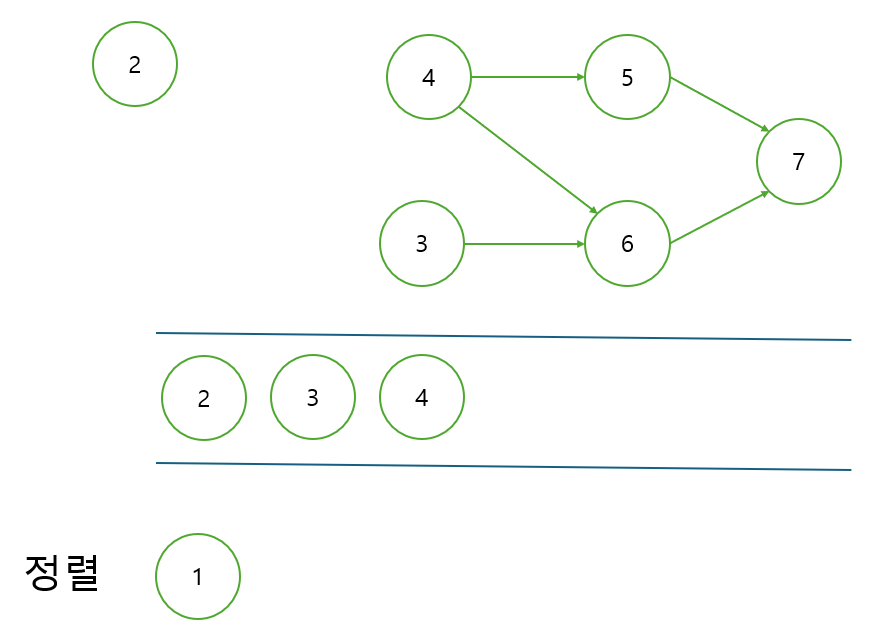
조금 더 진행하여 노드 3까지 주변 간선을 제거한 경우를 살펴보자.
위의 경우는 3번 과목은 이수했지만 4번 과목을 아직 이수하지 않았다. 따라서 6번 과목의 진입 차수가 아직 0이 아니므로 큐에 담을 수 없다. 4번 과목을 이수하여 간선이 제거된다면 5번 과목과 6번 과목은 진입차수가 0이 되어 큐에 담을 수 있다.
사이클의 존재 여부
이 방법으로 사이클이 존재하는 지도 확인할 수 있다. 사이클 내의 노드는 절대 진입차수가 0이 될 수 없으므로 모두 방문하지 않았는데 큐가 비게 된다면 사이클이 있다고 판단할 수 있다.
시간 복잡도
노드의 수가 V 간선의 수가 E라고 하자. 모든 노드를 한 번씩 거치고 모든 간선은 한 번씩 제거되는 과정을 거친다. 따라서 시간 복잡도는 O(V + E)이다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public class Main {
static List<List<Integer>> nearEdgeInfo = new ArrayList<>();
static int N;
static int M;
static int[] inDegree;
public static void main(String[] args) throws Exception {
N = getNodeNumber();
M = getEdgeNumber();
inDegree = new int[N]; //진입차수 저장
nearEdgeInfo = getEdgeInfo();
//nearEdgeInfo에서 간선의 dest 수로 진입 차수를 얻을 수 있다.
inDegree = getInitialInDegree();
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < N; i++) {
//진입차수가 0이면 큐에 추가
if (inDegree[i] == 0) {
queue.add(i);
inDegree[i] = -1; //방문한 노드 처리
}
}
StringBuilder sb = new StringBuilder();
while (!queue.isEmpty()) {
//큐에서 하나를 꺼낸다
int current = queue.poll();
sb.append(current+1).append(' '); //결과에 저장
List<Integer> currentNearEdgeInfo = nearEdgeInfo.get(current);
//간선을 제거하는 과정
//방향 그래프의 도착 노드의 진입차수를 1 감소시킨다.
for (int i : currentNearEdgeInfo) {
inDegree[i] -= 1;
}
//진입차수가 0인 노드를 큐에 추가한다.
for (int i = 0; i < N; i++) {
if (inDegree[i] == 0) {
queue.add(i);
inDegree[i] = -1;
}
}
}
System.out.print(sb);
}
}
결론
위상 정렬은 DAG에서 방문하는 순서를 결정하는 알고리즘이다. 이러한 위상 정렬은 두 노드 사이에 의존성이 있거나 먼저 수행해야 하는 제약 사항이 존재할 때 어떤 순서로 실행할 지와 관련된 상황에서 활용할 수 있다.
다음 포스트에서는 위상 정렬을 이용한 그래프의 최장 거리 탐색을 알아볼 예정이다.
연관 문제
Reference
https://velog.io/@kimdukbae/%EC%9C%84%EC%83%81-%EC%A0%95%EB%A0%AC-Topological-Sorting https://blog.encrypted.gg/1020 https://math.stackexchange.com/questions/113288/etymology-of-topological-sorting