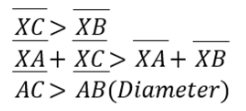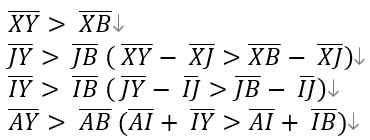백준 1167 트리의 지름 Java(+ 증명)
알고리즘 분류 : 그래프 이론, 그래프 탐색, 트리, 깊이 우선 탐색
https://www.acmicpc.net/problem/1167
요약
모든 노드 사이의 거리를 그래프 탐색으로 구해서 최장 거리를 찾을려고 하면 시간 초과가 발생하는 문제이다. 트리에서 임의의 한 점에서 가장 먼 지점은 트리 지름의 시작점이다는 점을 알고 있으면 임의의 한 점에서 가장 먼 지점을 그래프 탐색으로 한번, 트리 지름의 시작점에서 끝점을 그래프 탐색으로 한번 총 두 번의 그래프 탐색만으로 트리 지름을 구할 수 있다. 이 방식이 어떻게 가능한지에 대한 증명도 아래에 서술한다.
풀이
트리에서 임의의 한 점에서 가장 먼 지점은 트리 지름의 시작점이다
이 명제를 알고 있으면 아주 쉽게 풀 수 있는 문제다. DFS나 BFS를 두번 수행하면 되므로 코드 작성은 어렵지 않다. 하지만 이 명제가 왜 반례가 없는지 개인적으로 궁금증이 생겨 찾아보고 정리하였다. 바로 코드 풀이를 보고 싶다면 넘어가면 된다. 증명은 이 글을 참고하여 정리하였음을 미리 밝힌다.
귀류법은 p -> q가 참임을 증명하기 위해 p -> ~q는 거짓이다를 보여야 한다. 여기서 p는 “임의의 점 X에서 가장 먼 점”, q는 “트리 지름의 양 끝점 중 한 점”이다. 이 때 모든 케이스를 두 가지로 분류할 수 있다.
- X는 트리의 지름 경로 내부에 있다.
- X는 트리의 지름 경로 외부에 있다.
임의의 점 X가 트리 지름 경로 내부에 있는 경우
이 트리는 AB가 트리의 지름이다. X가 트리 지름 경로 내부에 있으므로 AB = AX + XB이다. 귀류법으로 X에서 가장 먼 점이 트리 지름의 끝 점이 아닌 또 다른 점 C라고 가정하자. 이 가정을 바탕으로 다음 식을 만족한다. X에서 A보다 B가 더 멀다고 가정한다. A가 더 먼 경우 A와 B의 이름을 바꾸면 된다.
트리 지름보다 더 긴 경로(AC)가 있으므로 트리 지름의 정의에 모순된다. 따라서 X에서 가장 먼 점은 트리 지름의 한 점인 B가 맞다.
임의의 점 X가 트리 지름 경로 외부에 있는 경우
아래 나오는 트리들은 모두 AB가 트리의 지름이다. 점 X가 경로 외부에 있을 때 또 두 가지 케이스로 세분화할 수 있다.
(여기서 교차는 두 경로 사이에 공유하는 점이 존재한다는 의미)
- X에서 가장 길이가 긴 경로는 트리 지름 경로와 교차한다.
- X에서 가장 길이가 긴 경로는 트리 지름 경로와 교차하지 않는다.
결론부터 말하면 X에서 가장 길이가 긴 경로가 트리의 지름과 교차하지 않는 경우는 없다. 트리의 지름을 교차하는 경우는 무조건 X에서 가장 길이가 긴 경로가 트리의 지름 중 한 점이 된다.
교차하지 않는 경우
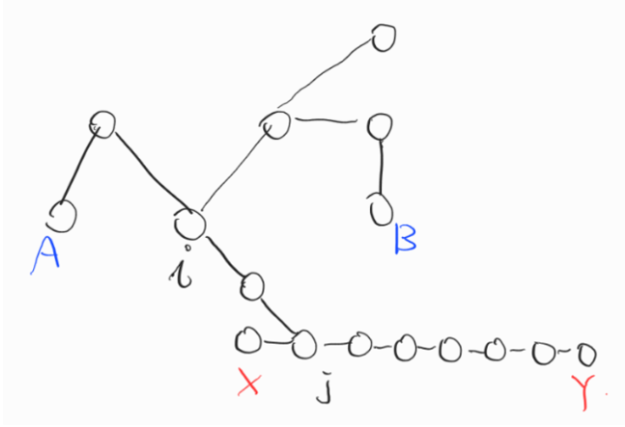
트리 지름 경로와 교차하지 않는 경우가 왜 존재하지 않는지 살펴보자. 이 그래프는 트리 경로(AB)와 X에서 가장 길이가 긴 경로(XY)는 교차하지 않는다. 이 때 j에서 Y가 X보다 더 멀다고 가정한다. X가 더 멀다면 X와 Y의 이름을 바꾸면 된다.
X에서 Y까지의 거리는 X에서 B까지의 거리보다 더 길다. 만약 X에서 Y보다 B가 더 멀었다면 Y가 아닌 B를 선택했을 것이다. 이를 바탕으로 다음 식을 만족한다.
트리 지름보다 더 긴 경로(AY)가 있으므로 트리 지름의 정의에 모순된다. 따라서 X에서 가장 길이가 긴 경로가 트리 지름을 교차하지 않는 경우는 존재하지 않는다.
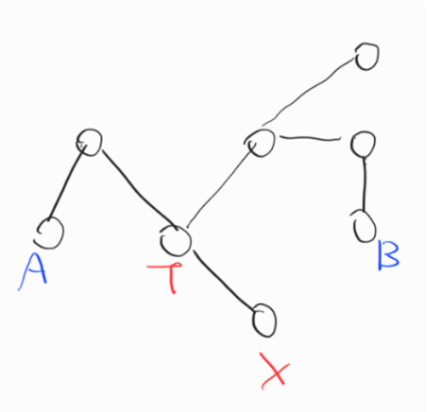
교차하는 경우
T는 트리 지름 경로 내부에 있으므로 T에서 가장 먼 점은 A나 B임을 이전 증명에서 확인할 수 있다. 이 때 X에서 가장 먼 경로는 XT + (T에서 가장 먼 경로)이므로 X에서 가장 먼 점이 A나 B임을 쉽게 확인할 수 있다. 위와 같은 증명으로 임의의 한 점에서 가장 먼 점은 트리 지름의 한 점임을 보일 수 있다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int V;
static List<Map<Integer, Integer>> nearNodes = new ArrayList<>();
public static void main(String[] args) throws Exception {
//입력 받기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
getInput(br);
//임의의 점은 0으로 설정후 BFS
int[] firstResult = BFS(0);
//찾은 점에서 BFS로 트리 길이 구하기
int[] secondResult = BFS(firstResult[0]);
System.out.println(secondResult[1]);
}
static void getInput(BufferedReader br) throws Exception {
V = Integer.parseInt(br.readLine());
for (int i = 0; i < V; i++) {
nearNodes.add(new HashMap<>());
}
for (int i = 0; i < V; i++) {
int[] line = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int j = 1;
while (line[j] != -1) {
//모든 인덱스는 1을 빼고 저장
nearNodes.get(line[0] - 1).put(line[j] - 1, line[j+1]);
j += 2;
}
}
}
static int[] BFS(int start) {
int maxDistance = 0;
int maxIndex = start;
boolean[] isVisited = new boolean[V];
LinkedList<Node> queue = new LinkedList<>();
queue.add(new Node(start, 0));
while (!queue.isEmpty()) {
Node current = queue.removeFirst();
Map<Integer, Integer> nearNodeInfo = nearNodes.get(current.index);
isVisited[current.index] = true;
if (maxDistance < current.distanceFromStart) {
maxDistance = current.distanceFromStart;
maxIndex = current.index;
}
for (Map.Entry<Integer, Integer> e : nearNodeInfo.entrySet()) {
int nearNodeIndex = e.getKey();
if (!isVisited[nearNodeIndex]) {
queue.add(new Node(nearNodeIndex, current.distanceFromStart + e.getValue()));
}
}
}
return new int[]{maxIndex, maxDistance};
}
static class Node {
int index;
int distanceFromStart;
Node(int index, int distanceFromStart) {
this.index = index;
this.distanceFromStart = distanceFromStart;
}
}
}
이 문제에서 주의할 점이 어디에서도 V개의 줄에 걸쳐 간선의 정보가 순서대로 주어진다는 말은 없다. 따라서 순서대로 입력을 받았다간 틀렸습니다라는 결과를 얻을 것이다. 이 점만 조심하면 크게 주의할 부분은 없다.
Reference
https://medium.com/@tbadr/tree-diameter-why-does-two-bfs-solution-work-b17ed71d2881