DB - 인덱스 기본 동작 원리와 설정 기준

Posted Aug 28, 2024 Updated Sep 12, 2024

By MilkTea24 21 min read

데이터베이스 스터디 3주차에서 학습하고 정리한 내용입니다.

1. 랜덤 I/O와 순차 I/O

하드 디스크에서 랜덤 I/O와 순차 I/O

하드 디스크(HDD)는 데이터를 저장하고 읽기 위한 기계 장치인 ‘헤더’가 존재한다. 특정 위치의 데이터를 읽거나 쓰기 위해서는 디스크 원판을 돌리고 이 헤더를 물리적으로 직접 옮겨주어야 한다. 이 물리적인 과정은 CPU의 클럭 등에 비해 매우 많은 시간이 소요된다. 그래서 많은 데이터베이스 서버에서는 항상 디스크 장치가 병목이 발생한다.

이 병목을 줄이기 위해서는 원판을 돌리고 헤더를 옮기는 과정을 최대한 줄이는 것이 핵심이다. 데이터 3개를 읽고 쓸 때 디스크 내 흩어진 위치에 데이터를 읽고 쓰는 과정을 랜덤 I/O라고 한다. 반면 3개의 데이터를 인접한 위치에 순차적으로 기록할 때 순차 I/O라고 한다. 순차 I/O는 물리적인 과정이 많이 줄어드므로 랜덤 I/O에 비해 I/O 속도가 향상된다.

SSD에서 랜덤 I/O와 순차 I/O

SSD는 이러한 물리적인 장치가 존재하지 않으므로 랜덤 I/O와 순차 I/O 모두 성능이 동일하다고 생각할 수도 있다. 하지만 SSD 또한(하드디스크 만큼의 큰 차이를 보이진 않지만) 순차 I/O가 더 좋은 성능을 보인다. SSD 또한 컨트롤러가 흩어진 메모리에 있는 데이터를 읽는데 약간의 오버헤드가 존재하고 최적화 가능성이 낮아지기 때문이다.

랜덤 I/O 줄이기

이러한 랜덤 I/O를 순차 I/O로 바꿔서 실행할 방법은 그다지 많지 않다. 꼭 필요한 데이터만 조회함으로써 랜덤 I/O 자체를 줄이는 과정을 통해 성능을 향상시킬 수 있다.

2. 인덱스

인덱스는 책의 찾아보기와 비슷한 기능을 수행한다. 어떠한 데이터를 찾을 때 책의 전체 내용을 처음부터 끝까지 보지 않고 찾아보기를 활용하면 해당하는 페이지를 바로 찾을 수 있다. 또한 책의 찾아보기의 단어들은 정렬되어 있어 원하는 단어가 몇페이지에 있는지 빨리 찾을 수 있다.

데이터베이스의 인덱스도 마찬가지이다. 인덱스는 키-값 쌍으로 구성되어 있으며 찾고자 하는 데이터가 키, 이 데이터의 주소가 값이 된다. 또한 키는 정렬되어 있어 원하는 데이터의 위치를 더욱 빨리 찾을 수 있다.

하지만 이러한 정렬된 키-값 쌍 자료구조는 항상 정렬된 상태를 유지해야 하므로 삽입, 수정, 삭제 시 정렬되지 않은 구조에 비해 더 많은 비용이 든다. 따라서 인덱스는 삽입, 수정, 삭제 비용을 희생한 대신 조회 비용을 줄일 수 있는 구조이다.

3. 인덱스의 동작 방식

여러 구현 방식이 있지만 B-Tree 자료 구조를 이용한 방식과 해싱을 이용한 방식이 있다.

B-Tree

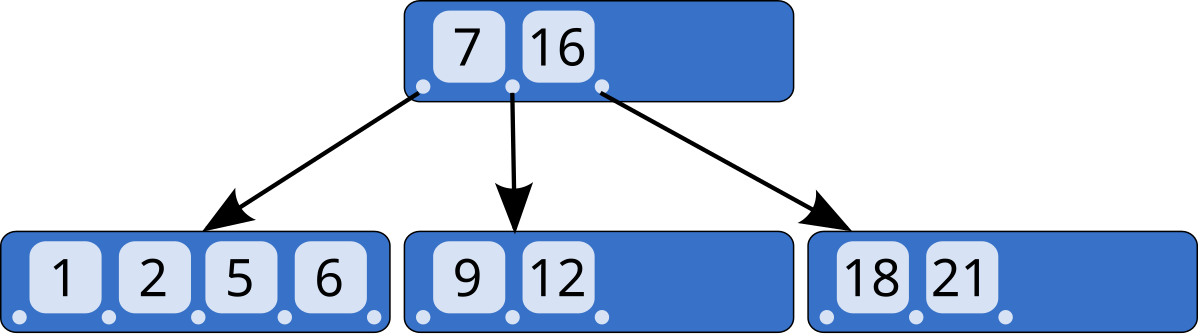
B-Tree는 가장 범용적인 목적으로 사용하는 인덱스 알고리즘이다. B-Tree는 Balanced Tree의 약자로 루트 노드에서 리프 노드까지 길이가 모두 일정하다.(균형이 맞춰져 있다) 로그 시간 복잡도 내에 정렬된 상태를 유지하며 삽입, 삭제, 수정할 수 있다.

구조

B-Tree는 하나의 루프 노드가 존재하고 가장 하위의 노드는 리프 노드라 한다. 루프 노드와 리프 노드 사이 중간 노드는 브랜치 노드라 한다.

B-Tree 인덱스 키 추가

노드에 저장된 데이터가 일정 크기를 넘어 더이상 데이터를 저장할 수 없는 경우 이 노드를 분할하는 작업을 수행한다. 단순히 리프 노드만 분리되는 것이 아닌 리프 노드 분할 후 브랜치 노드도 일정 크기를 초과하였다면 브랜치 노드도 분할해 주어야 한다.

인덱스에 키를 추가할 때 비용은 테이블의 컬럼 수, 컬럼의 크기, 인덱스의 컬럼 특성에 따라 달라지지만 러프하게 테이블에 데이터를 추가하는 작업 비용 대비 1.5배가 소요된다고 한다. 따라서 인덱스가 없는 테이블의 삽입 비용이 1이면 인덱스가 한 개 있는 테이블의 삽입 비용은 2.5(1 + 1.5)로 예측한다.

B-Tree 인덱스 키 삭제

B-Tree의 키 값이 삭제되는 경우 해당 키 값이 저장된 B-Tree의 리프 노드를 찾아서 그냥 삭제로 표시만 하면 된다. 삭제로 표시하는 과정은 디스크 I/O가 필요하므로 최신 InnoDB에서는 이를 지연 처리하는 기능도 제공한다.

B-Tree 인덱스 키 수정

B-Tree는 정렬된 구조이므로 트리의 구조 변경 없이 키 값만 바꾸는 것은 불가능하다. 수정할 키 값을 삭제한 후 다시 새로운 키 값을 추가하는 형태로 처리한다.

B-Tree 인덱스 키 검색

B-Tree는 100% 일치하는 데이터 뿐만 아니라 정렬된 구조이므로 prefix로도 검색할 수 있다. 하지만 집계 함수나 연산 등으로 값이 변형된 경우 B-Tree 인덱스에 존재하는 값이 아니므로 활용할 수 없다.

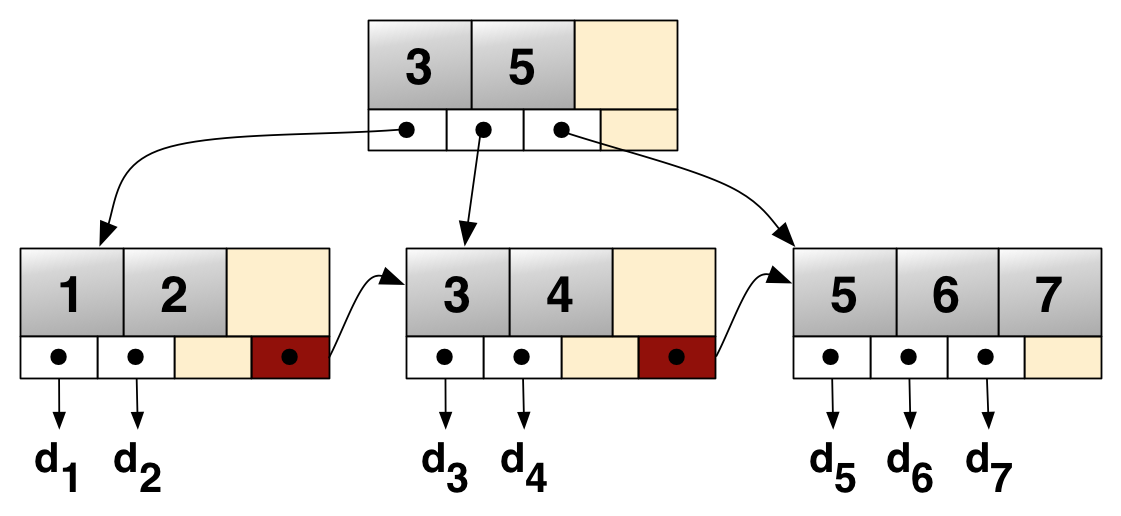
B+Tree

B-Tree를 더 개선한 자료 구조이다. B+Tree는 리프 노드에만 데이터가 존재하고 리프 노드들은 LinkedList 형태로 연결되어 있다. 이는 범위 탐색에서 유리한데 B-Tree는 범위 내 데이터를 트리에서 탐색해야 하지만 B+Tree는 리프 노드로 이동 후 LinkedList 자료 구조를 활용하여 **순차 접근을 할 수 있다.

해싱

Log Structured File 기반 Hash 인덱스와 이를 발전시킨 Lsm-Tree에 대한 설명은 여기를 참고하면 된다. 해시 인덱스는 Java의 HashMap처럼 해시 알고리즘을 바탕으로 값과 이에 해당하는 주소를 매핑한다. 해시 인덱스 방식은 탐색 속도가 O(1)에 근접하여 좋은 성능을 보여주나 해시 값이 정렬되어 있지 않아 범위 탐색 등은 불가능하다.

4. 테이블 인덱스 설정 기준

인덱스는 동작 방식에서 살펴본 것처럼 인덱스를 유지하기 위해서는 추가적인 비용이 필요하다. 따라서 아무렇게나 인덱스를 설정한다면 인덱스를 설정하지 않은 경우보다 오히려 느릴 수 있다. 인덱스를 설정할 때 필요한 몇 가지 고려 사항을 살펴보자.

1) 인덱스 키 값의 크기

디스크의 읽기, 쓰기 작업의 최소 단위를 페이지라고 한다. 인덱스 또한 디스크의 저장이 필요한 데이터이므로 페이지 단위로 관리된다. B-Tree 인덱스에서 하나의 노드는 페이지 단위로 구성되어 하나의 노드 내 데이터는 한 번의 디스크 I/O로 가져올 수 있다.

기본 페이지 크기가 16KB이고 주소 값의 크기가 12바이트인 데이터베이스가 있다고 하자. 만약 인덱스의 키가 16바이트라면 하나의 페이지 안에 몇 개의 키를 저장할 수 있을까?

10 * 1024 / (16 + 12) = 585개를 저장할 수 있다.

인덱스의 키가 32바이트라면 10 * 1024 / (32 + 12) = 372개를 하나의 페이지 안에 저장할 수 있다.

똑같이 500개 데이터를 읽더라도 인덱스의 키가 16바이트라면 한 번의 페이지를 읽어서 해결할 수 있지만 인덱스의 키가 32바이트라면 페이지를 두 개 일겅야 한다. 결국 인덱스 키 값의 크기가 늘어나면 디스크로부터 읽어야 하는 횟수가 늘어나고 그만큼 느려진다.

인덱스 키의 크기가 증가하면 인덱스 전체 크기가 증가하기 때문에 메모리에 캐시할 수 있는 레코드 수 또한 줄어들게 된다. 데이터의 크기가 너무 크면 인덱스 효율이 떨어질 수도 있다는 말이다.

2) B-Tree 깊이

B-Tree의 깊이가 길어지면 거쳐야하는 브랜치 노드가 많아지기 때문에 디스크를 읽는 횟수가 늘어난다. 따라서 깊이가 얕은 경우 더 효율적으로 인덱스를 활용할 수 있다.

B-Tree 깊이는 개발자가 직접 제어할 수는 없지만 인덱스 키 값의 크기와 밀접한 관계가 있다. 앞의 예시에서 B-Tree의 깊이가 3이라도 인덱스의 크기에 따라 저장할 수 있는 데이터의 수가 달라진다. 키 값이 16바이트인 경우 585 * 585 * 585로 최대 2억개의 키 값을 담을 수 있지만 32바이트인 경우 372 * 372 * 372로 5천만 개의 키 값을 담을 수 있다. 따라서 동일한 2억개의 키를 저장하더라도 키 값이 32바이트면 B-Tree의 깊이가 3보다 증가하여 디스크 읽기 횟수가 증가하게 된다.

인덱스 키 값의 크기는 노드 내 저장할 수 있는 데이터 수뿐만 아니라 깊이에도 영향을 미치기 때문에 최대한 작게 유지하는 것이 좋다.

3) 선택도(Selectivity)와 기수성(Cardinality)

두 단어 모두 거의 같은 의미로 사용되며 모든 인덱스 키 값 가운데 유니크한 값의 수를 의미한다.

id	state	city	street_name
1	NY	New York City	Broadway
2	CA	Los Angeles	Sunset Boulevard
3	IL	Chicago	Michigan Avenue
4	TX	Houston	Westheimer Road
5	CA	Los Angeles	Hollywood Boulevard
6	NY	New York City	Fifth Avenue
7	CA	San Francisco	Lombard Street

위의 테이블에서 유니크한 값은 NY, CA, IL, TX이므로 기수성은 4이다. 만약에 중복된 값이 많아지면 기수성은 낮아지고 선택도 또한 떨어진다. 인덱스는 선택도가 높을수록 검색 대상이 줄어들기 때문에 빠르게 처리할 수 있다.

위의 테이블에서 전체 레코드 건수는 1만 건이고 state 칼럼으로만 인덱스가 생성된 상태에서 아래 두 케이스를 살펴보자.

A 케이스 : state 칼럼의 유니크한 값의 개수가 10개
B 케이스 : state 칼럼의 유니크한 값의 개수가 1000개

  
SELECT * FROM address WHERE state = 'CA' AND city = 'Los Angeles';

A 케이스를 생각해보자. 유니크한 값의 개수가 10개이므로 각 유니크한 값마다 평균적으로 1000개가 있다고 추측할 수 있다. 이 경우 인덱스로 ‘CA’ state를 찾아도 데이터가 1000개가 조회되었으므로 이 1000개 데이터의 city가 ‘Los Angeles’인지 확인해야 한다.

B 케이스는 유니크한 값의 개수가 1000개이므로 각 유니크한 값마다 평균적으로 10개가 있다고 추측할 수 있다. 이 떄 인덱스로 ‘CA’ state를 찾으면 데이터 10개가 조회되었으므로 10개 데이터만 확인하면 된다.

이처럼 동일한 쿼리더라도 기수성에 따라 서버가 수행한 작업은 큰 차이를 보이므로 가수성이 높은 컬럼을 인덱스로 채택할 때 효율이 좋다.

4) 읽어야 하는 레코드의 건수

1000개의 데이터가 저장되어 있는 테이블에서 800개의 데이터를 조회한다고 가정하자. 이 경우 인덱스를 통해 조회하는 것보다 전체 테이블을 스캔하는 방법이 더 빠를 수도 있다.

얼마나 많은 데이터를 조회할 때 인덱스보다 직접 조회하는 일이 효율적인지는 MySQL 옵티마이저를 통해 알 수 있다. MySQL 옵티마이저는 인덱스를 통해 레코드 1건을 읽는 것이 직접 읽는 것보다 4~5배 비용이 더 많이 드는 작업인 것으로 예측한다. 100건의 데이터가 있을 때 50건의 데이터를 인덱스로 읽으면 전체 테이블을 스캔하여 필터링하는 과정보다 더 많은 비용이 드는 것이다. 따라서 조회하려는 데이터가 전체 테이블 레코드의 20~25%를 넘어서면 테이블을 모두 스캔하여 필요하나 데이터만을 가져오는 방식이 더 효율적이다.

5. 테이블에 인덱스를 많이 설정하면 좋을까?

Real MySQL 8.0에 따르면 인덱스가 없는 테이블의 삽입 비용이 1일 때 인덱스가 하나 추가될 때마다 1.5의 추가적인 비용이 든다고 한다. 또한 조회 시에도 인덱스를 통해 레코드 1건을 읽는 것이 직접 테이블 내에서 레코드 1건을 읽는 것보다 4~5배 비용이 더 많이 든다. 다만 인덱스를 활용하면 전체 테이블을 스캔할 필요가 없기 때문에 조회 시 더 빠른 성능을 보이는 것이다.

따라서 인덱스를 설정하는 일은 추가적인 오버헤드를 야기하므로 필수적인 컬럼에만 인덱스를 설정해야 한다. 인덱스를 효율적으로 설정할 수 있는 예시는 다음과 같다.

삽입, 삭제, 수정보다 조회 작업이 더 많은 비중을 차지하는 경우
기수성이 높은 컬럼에서 조회가 많은 경우
전체 데이터를 조회하는 일은 거의 없고 단건 조회나 작은 범위의 조회가 잦은 컬럼인 경우

Reference

백은빈, 이성욱 편저, Real MySQL 8.0, 위키북스

3

B-Tree 이미지 출처: By CyHawk - Own work based on [1]., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=11701365

https://zorba91.tistory.com/293

B+Tree 이미지 출처: By Grundprinzip - 자작, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=10758840

Database

Index

This post is licensed under CC BY 4.0 by the author.